AVALIAÇÃO TEÓRICA DA AFINIDADE RELATIVA DE INIBIDORES DE TROMBINA VIA PERTURBAÇÃO DA ENERGIA LIVRE

Cristiano Ruch Werneck Guimarães* (PG) & Ricardo Bicca de Alencastro (PQ)

Laboratório de Modelagem Molecular, Departamento de Química Orgânica,
Instituto de Química, Universidade Federal do Rio de Janeiro, Cidade Universitária, Bloco A, lab. 609, Rio de Janeiro, RJ 21949-900

e-mail:cris@pc142.iq.ufrj.br

palavras-chave: inibidores de trombina, dinâmica molecular, perturbação da energia livre

A trombina é uma serinil-protease que desempenha papel central na coagulação sangüínea. Esta enzima é responsável pela conversão do fibrinogênio em fibrina, sendo também o estimulante mais potente da agregação plaquetária. Desta forma, sua inibição tornou-se o alvo principal no desenvolvimento de novos agentes antitrombóticos. Dentre os inibidores do centro ativo, podemos citar a benzamidina¹ e a 4-(3-carbóxi-2-oxo-1-propil)-benzamidina.¹ No presente trabalho, apresentamos resultados parciais da avaliação da diferença de energia livre de complexação à trombina destes inibidores e entre estes e novos candidatos. Para isto, adotamos a estratégia do cálculo de energia livre relativa entre dois estados, empregando o algoritmo FDTI² (Discover 2.9.7-InsightII-MSI). A diferença de energia livre da transformação entre dois estados (DAtransf.) pode ser descrita pela equação:

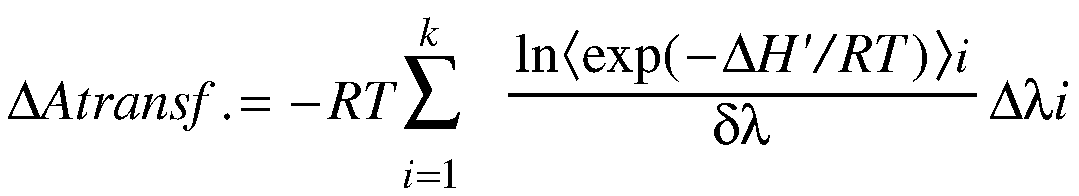
em que R é a constante dos gases, T é a temperatura absoluta, DH’ = H_li+dl – H_li ,
< >_i refere-se à média em relação a um ensemble N,V,T do estado representado pelo Hamiltoniano H_li , l é o parâmetro de acoplamento, k é o número de quadraturas e Dl_i é um valor que depende do esquema de integração numérica usado. O parâmetro de acoplamento l introduzido no método FDTI quebra o cálculo de energia livre em janelas, cada qual envolvendo um intervalo suficientemente pequeno em l para propiciar um bom recobrimento no espaço de fase e, assim, permitir que a energia livre seja calculada acuradamente. Este parâmetro pode variar de 0 (100% do estado inicial) a 1 (100% do estado final). Em alguns casos, quando a diferença estrutural entre os dois estados é significativa, além da introdução do parâmetro de acoplamento l para cada transformação, é necessário o uso de estados intermediários que permitam uma transformação estrutural mais suave. Deste modo, a estratégia descrita previamente permite a construção do ciclo termodinâmico abaixo, que viabiliza o cálculo de diferença de energia livre de complexação à trombina entre os dois inibidores citados acima. No ciclo termodinâmico, podemos verificar que só são necessárias as quantidades DAtransf.i(comp.) e DAtransf.i(sol.), transformação i no complexo solvatado e em

solução, para o cálculo da diferença de energia livre de complexação (DDAcomp.) entre os inibidores.

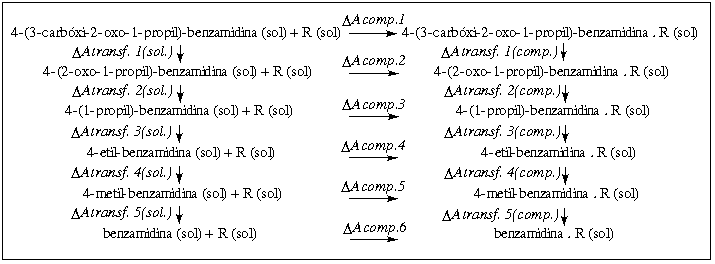
As transformações foram realizadas usando técnicas de dinâmica molecular em condições N,V,T (T = 300 K), aplicando o modelo de solvatação esférico
(r = 16 Å). Empregamos um potencial semi-harmônico (k = 0,5 kcal/mol Ų para
r > 16 Å) para prevenir a "evaporação" do solvente, um corte esférico de 11 Å para as interações não ligadas e o campo de força CVFF.³ Os resultados de DDAcomp encontram-se dentro da ordem de grandeza esperada para as transformações 2, 3, 4 e 5, o que não acontece para a transformação 1 (Tabela). Isto provavelmente é resultado da solvatação inadequada da carga positiva gerada na transformação 1. Assim, para permitir a comparação dos inibidores propostos no presente trabalho com o inibidor 4-(3-carbóxi-2-oxo-1-propil)-benzamidina, a transformação 1 será repetida com um modelo de solvatação esférico de maior raio. Apesar disto, com os resultados das transformações 2, 3, 4 e 5 podemos verificar que com exceção do inibidor 4-metil-benzamidina, todos os novos candidatos são melhores que a benzamidina.

1 - Babine, R. E. & Bender, S. L., 1997 Chem. Rev., 97 (5), 1359.

2 - Mezei, M. et al., 1986 Ann. N. Y. Acad. Sci., 482, 1.

3 - Dauber-Osguthorpe, P. et al., 1988 Proteins: Struct. Funct. Gen., 4, 31.

(FAPERJ, CNPq)