UTILIZAÇÃO DE PROGRAMAS ALGÉBRICOS NA CONSTRUÇÃO E VISUALIZAÇÃO DE ORBITAIS HIDROGENÓIDES
Jean-Jacques De Groote (PQ) e Marian Rosaly Davolos (PQ)
Departamento de Química Geral e Inorgânica – Instituto de Química de Araraquara
UNESP
palavras-chave: Programas Algébricos, Visualização de Orbitais, Computação Simbólica.
Os programas Algébricos, que vem se tornando uma ferramenta fundamental para a pesquisa científica, também podem ser aplicados com grandes vantagens no auxílio ao ensino. Esta classe de programas permite a manipulação simbólica e numérica de expressões matemáticas e, em versões mais difundidas como o Mathematica, Reduce e Maple, também são intrumentos úteis para a elaboração e manipulação de gráficos em duas e três dimensões.
Neste trabalho utilizamos o programa Maple1 para a construção e análise das soluções da equação de Schrödinger do átomo de Hidrogênio e, em particular, da combinação dos orbitais na construção de estados híbridos. O objetivo principal deste estudo é a construção de um algoritmo que permita ao aluno relacionar diretamente a formulação matemática de funções de onda com sua representação espacial. Este recurso é um complemento util aos livros texto, especialmente de Química Geral e Inorgânica, por permitir uma interação dinâmica como por exemplo na modificação de funções e na rotação de imagens tri-dimensionais.
Como uma descrição inicial de aplicação de manipulação simbólica, mostramos abaixo um exemplo de uma simples expansão em série de Taylor da função
![]()
em torno da origem:
> taylor( f, x, 6);
![]()
![]()
O resultado é obtido em forma de símbolos, em contraposição aos programas tradicionais, que utilizam linguagens como Basic, Fortran, Pascal, etc… , fornecendo apenas valores numéricos. A obtenção de valores numéricos também é possivel com precisão arbitrária utilizando, no ambiente Maple, o comando específico: evalf.
Para o caso de soluções de estados quânticos hidrogenóides, podemos combinar a descrição algébrica da função de onda radial, por exemplo, do estado 2s (em unidades atômicas), e sua representação gráfica:
 R(2,0):=(sqrt(2)/4)*exp(-Z*r/2)*(2-r);
R(2,0):=(sqrt(2)/4)*exp(-Z*r/2)*(2-r);
r2
R22s
![]()
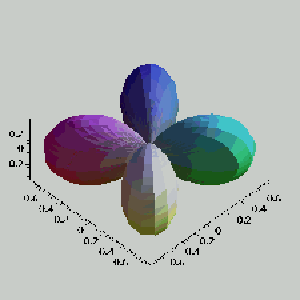
 Uma
aplicação mais interessante do ponto de vista de
descrever estados de dificil visualização é a
construção de orbitais atômicos. No exemplo
abaixo estão as representações das funções
de onda angular dos orbitais dxy e dz2
:
Uma
aplicação mais interessante do ponto de vista de
descrever estados de dificil visualização é a
construção de orbitais atômicos. No exemplo
abaixo estão as representações das funções
de onda angular dos orbitais dxy e dz2
:
Uma vez que as funções de onda angular estão definidas, torna-se possível sua
combinação, para formar orbitais híbridos, como por exemplo, sp2 e sp3,
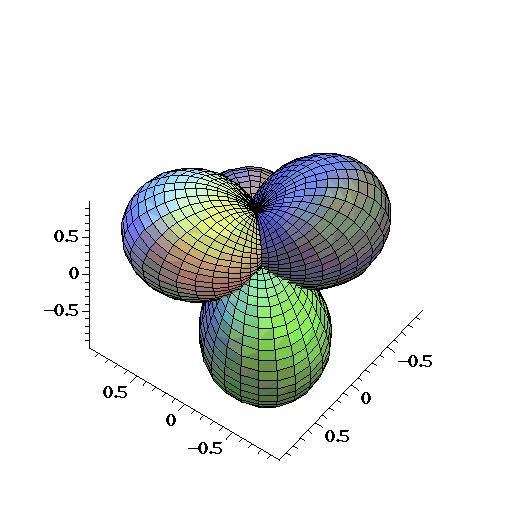
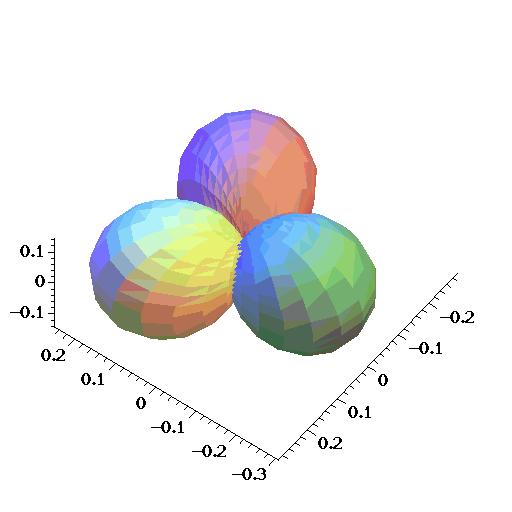
A possibilidade de rotacionar estas imagens em tempo real em pequenos computadores facilita a discussão sobre a estrutura espacial, e podem ser também utilizados recursos para definir cores específicas para amplitudes de probabilidade que estão relacionadas com valores positivos ou negativos das funções de onda. Também é possível a representação de estados que normalmente não são encontrados em livros texto quando sua projeção bi-dimensional não permite uma análise clara.
1. Introduction to Maple, Andre Heck, Ed.Hanover (1996).