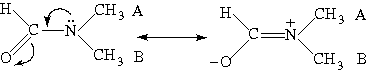
Figura 1: Formas canônicas de ressonância da dimetilformamida.
RMN DINÂMICA E CÁLCULOS COMPUTACIONAIS NA DETERMINAÇÃO DA BARREIRA ROTACIONAL DO N,N-DIMETILCARBAMATO DE CICLOEXILA.
Ernani Abicht Basso (PQ), Paulo Roberto de Oliveira (PG), Josiane Caetano (IC), Rodrigo Meneghetti Pontes (IC)
Departamento de Química – Universidade Estadual de Maringá (UEM)
Maringá – PR
palavras-chave: rmn dinâmica, cálculos computacionais, carbamatos
Quando núcleos trocam de um lado para outro entre duas posições A e B que apresentam valores de blindagem diferentes, o espectro de RMN deste núcleo pode ser afetado1. Um exemplo típico desta situação é observado no isomerismo rotacional das amidas (Figura 1).
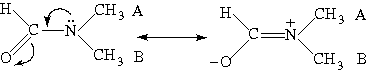
Figura
1: Formas canônicas de ressonância da dimetilformamida.
No espectro de RMN de 1H da dimetilformamida a 22,5oC dois sinais de metila são observados a d = 2,79 e 2,94. Acima dos 100oC estes sinais alargam-se e a 120oC coalescem. Aumentando a temperatura o sinal torna-se um pico estreito, sendo a posição deste exatamente o meio entre os dois picos observados a 22,5oC.
Embora uma grande variedade de estudos tenham sido realizados com as amidas, muito pouco é encontrado para os carbamatos. No presente trabalho investigou-se o isomerismo rotacional da porção amídica por RMN dinâmica e por cálculos computacionais.
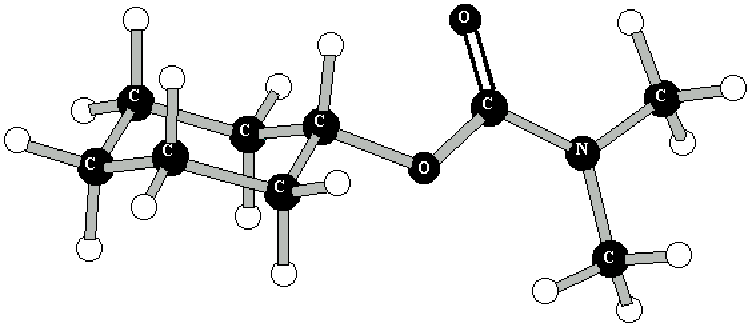
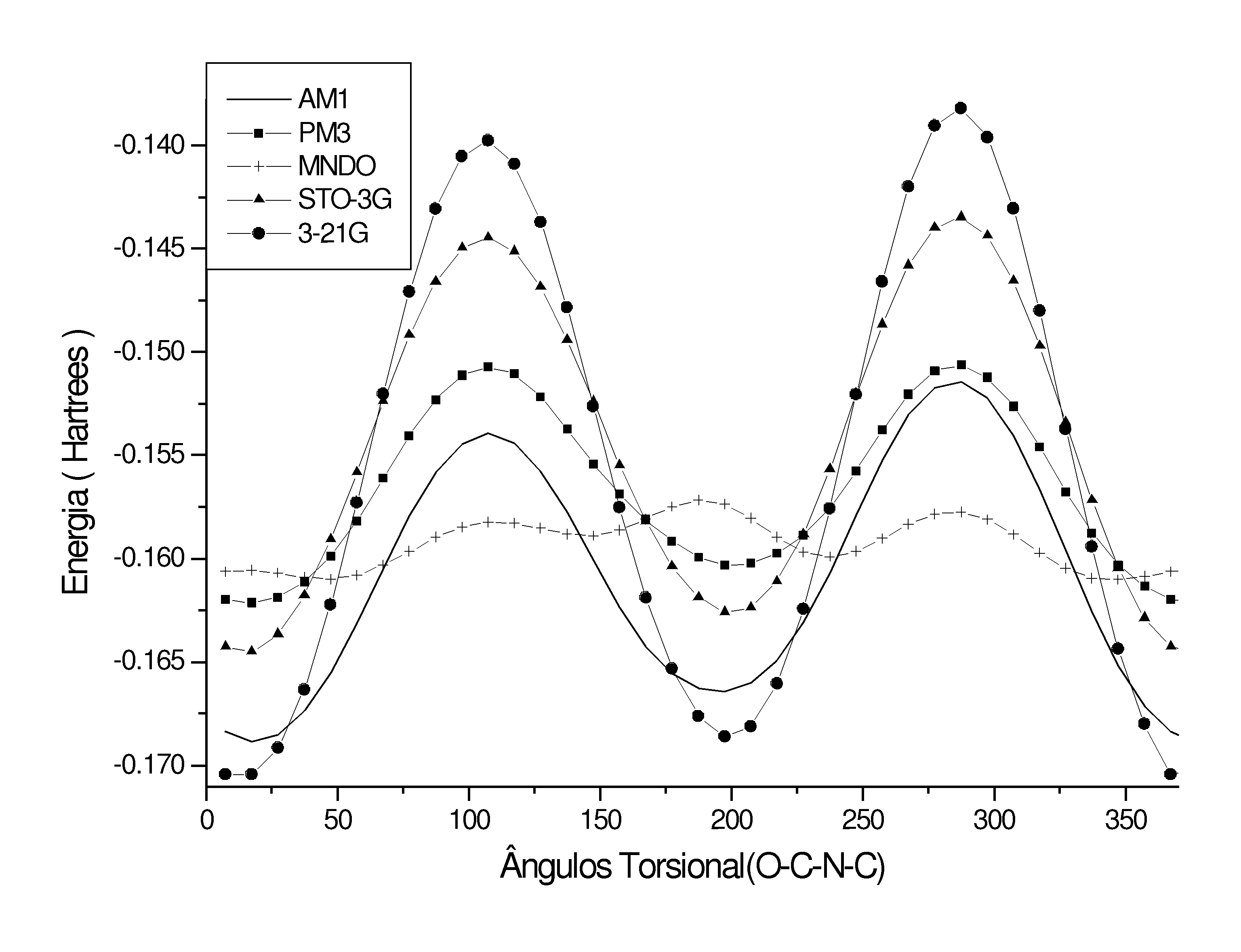
O N,N-dimetilcarbamato de cicloexila (Figura 2) foi investigado por RMND, adquirindo-se espectros de RMN de 13C em diferentes temperaturas. O composto foi também otimizado pelos métodos semi-empíricos (AM1, PM3 e MNDO) e Ab Initio (STO-3G e 3-21G). A estrutura obtida da otimização por cada um destes métodos foi submetida a um giro de 3600 conforme demonstrado na Figura 2. Os cálculos foram realizados com o programa GAUSSIAN-942.
Foram
realizados experimentos de RMN de 13C, em DMSO, a
temperaturas que variam de 20 0C à 70 0C.
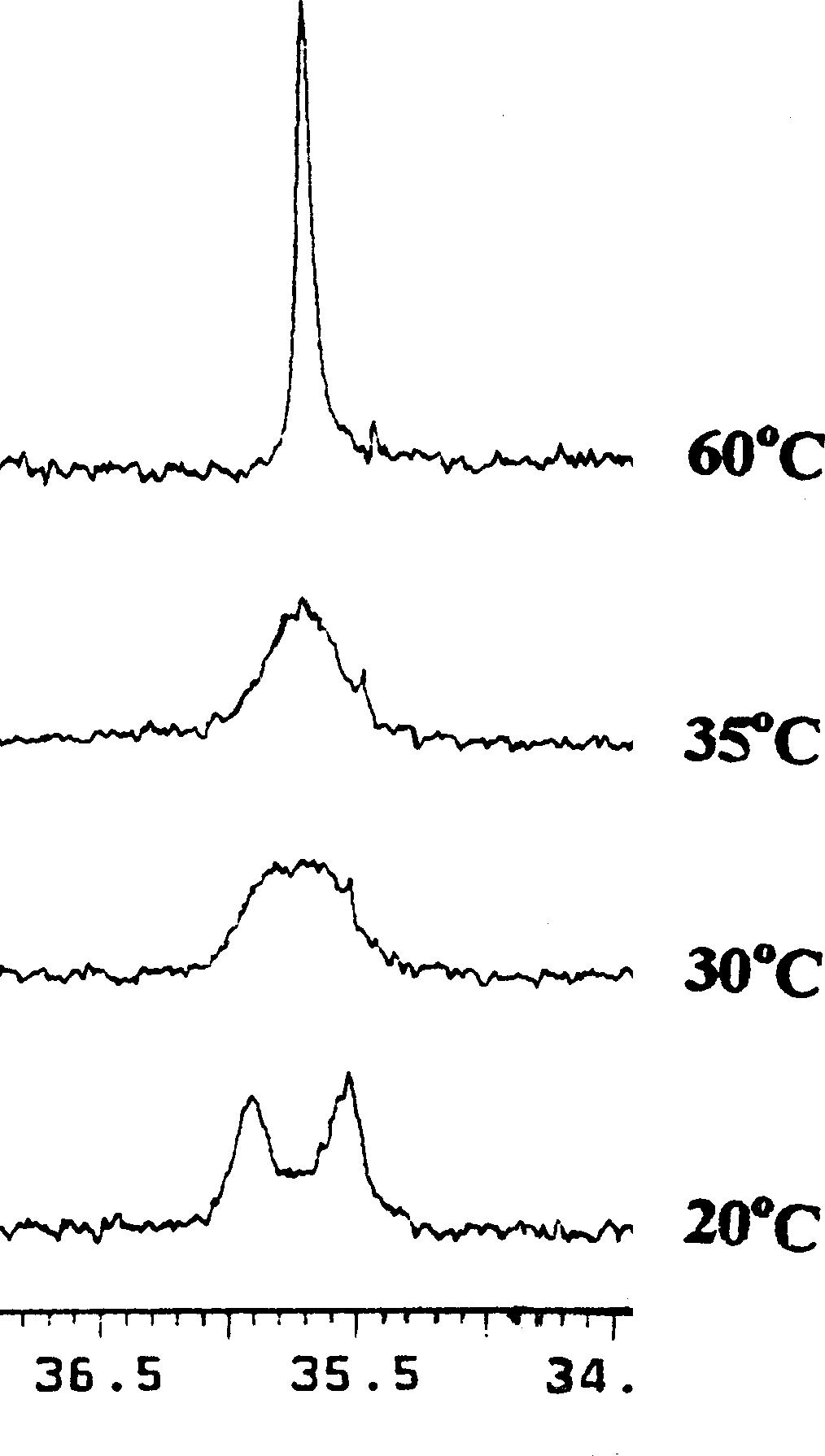
A 20 0C observa-se um sinal para cada uma das metilas, a
35 0C é atingido o ponto de coalescência e
acima desta temperatura o sinal começa a ficar mais estreito,
tornando-se um sinal único absorvendo no meio dos dois picos
originais observados a 20 0C. ( Ver Figura 3 ).
Figura 2. Variação da energia conformacional durante Figura 3. Espectro obtido
a rotação sobre o ângulo torsional (O-C-N-C). por RMND
Utilizando as equações abaixo determinou-se os valores da barreira rotacional (DG0) da porção amídica.
![]()
![]()
Paralelamente o composto foi otimizado pelos métodos semi-empíricos e ab initio. As estruturas otimizadas foram submetidas a um giro de 360o no ângulo torsional da porção amídica. Os resultados obtidos são apresentados na Tabela 1.
Tabela 1. Comparação dos valores de DG0 (kcal/mol) obtidos através dos cálculos computacionais com o obtido experimentalmente para o composto.
|
DGC(exp) |
DG (AM1) |
DG (PM3) |
DG (MNDO) |
DG (STO-3G |
DG (3-21G) |
|
15,4 |
9,4 |
7,2 |
1,5 |
12,6 |
19,3 |
Conclusões
O valore de DG0 obtido através do experimento de RMN dinâmica apresentou um valor inferior aos observados para as amidas, o que é esperado conforme dados da literatura3.
Este resultado mostrou-se pouco concordante com os obtidos pelos métodos semi-empíricos, entretanto apresentou uma concordância satisfatória com os resultados obtidos pelos cálculos ab initio.
1- Friebolin, H. “Basic One- and Two-Dimensional NMR Spectroscopy”, 2a Ed., VCH, New York, NY, 1993.
2- Foresman, A.B.; Frisch, A.; “Exploring Chemistry with Electronic Structure Methods”,.Second Edition, 1995 – 1996 .Gaussian, Inc.Pittsburgh, PA U.S.A
3- Cox, C.; Lectka, T.; J. Org. Chem. ,63, 2426-2427 (1998).