EFEITOS DE IMPUREZAS DOS GRUPOS 13 E 15 DA TABELA PERIÓDICA EM

EFEITOS DE IMPUREZAS DOS GRUPOS 13 E 15 DA TABELA PERIÓDICA EM CLUSTERS DE GERMANIO

Certas impurezas afetam drasticamente as propriedades elétricas de materiais semicondutores. A adição de Boro ao Silício numa proporção de 1 átomo de Boro para 10⁵ átomos de Silício aumenta a condutividade do silício puro na ordem de 10³ a temperatura ambiente [1]. Fato como este tem grande importância para o desenvolvimento de novos dispositivos eletrônicos e torna estes materiais uma fonte constante de investigação teórica [2] e experimental [3].

Neste trabalho verificamos o efeito de impurezas tais como: B, Al, Ga, In, N, P, As e Sb em clusters de Germânio com estruturas do tipo Ge₄YH₁₂ e Ge₃₄YH₃₆ (onde Y = impureza). As geometrias destes sistemas foram otimizadas em nível Hartree-Fock e empregando a Teoria do Funcional de Densidade com o funcional B3LYP, empregando-se um conjunto de base 6-311G e 6-311G* para todos os átomos, exceto para o Índio e Antimônio, nos quais foram empregado o conjunto de base LanL2dz. Nos clusters com 71 átomos, utilizou-se pseudopotencias de Hay e Wadt para representar os elétrons mais internos e reduzir o custo computacional.

A tabela 1 apresenta o efeito de algumas impurezas nos clusters Ge₃₄YH_36,em nível Hartree-Fock. Observa-se que os comprimentos das ligações entre os átomos de germânio e a impureza tendem a ser maiores na primeira esfera de coordenação e diminuem à medida que se afastam da impureza. Este comportamento sugere um efeito localizado ao redor da impureza. Também observa-se que as distâncias interatômicas obtidas entre Ge-Ga, Ge-Ge e Ge-As não seguem a tendência periódica dos respectivos raios atômicos, ou seja, a diminuição do raio atômico com o aumento de Z. Atribuímos este fato a uma maior concentração eletrônica sobre o átomo de As, enquanto sua vizinhança apresenta um acumulo de cargas positivas, desta forma, ocorre uma maior repulsão eletrônica entre os átomos vizinhos e conseqüentemente um aumento na ligação Ge-As, em relação a Ge-Ge.

Tabela 1 - Comprimentos de ligação Ge-Y (em Å), obtidos em nível Hartree-Fock, para espécies isoeletrônicas Ge₃₄YH₃₆.

A análise das cargas atômicas para os átomos de germânio e as diferentes impurezas foi avaliada através dos métodos de Mulliken e CHELPG. Alguns dos resultados obtidos são mostrados na figura 1.

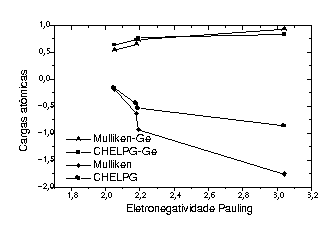
Figura 1 – Cargas atômicas de Mulliken e CHELPG sobre a impureza e os átomos de Germânio.

Na figura 1, observa-se que as cargas de Mulliken e CHELP apresentam tendências qualitativas semelhantes em relação a eletronegatividade (c) e ao número atômico (Z). Quantitativamente observa-se um comportamento distinto entre os valores de cargas e sua correlação com as propriedades analisadas, isto é, enquanto o método de Mulliken sugere que as cargas são transferidas de elementos menos eletronegativos (por exemplo, Ga c_P=1.81, q_M=-0.016), para elementos mais eletronegativos (Ge c_P=2,01,q_M=--0,365) de acordo com a escala de eletronegatividade de Pauling, no método CHELPG observa-se que as cargas são transferidas dos átomos de germânio para impureza.

A utilização de modelos de carga é extremamente difícil para permitir uma conclusão clara sobre o comportamento eletrônico de semicondutores dopados, uma vez que valores absolutos dependem significativamente do modelo a ser empregado para realizar-se os cálculos. No entanto, nossos resultados demonstram que os estados eletrônicos são modificados pela introdução de impurezas e permanecem localizados ao redor delas, e que, cálculos para clusters representam adequadamente o comportamento físico de um sólido, cujas propriedades eletrônicas são dominadas por efeitos de curto alcance.

BIBLIOGRAFIA

1 – C. Kittel; Introduction to Solid State Physics, ed. Jonh Wiley & Sons, 7^a edition, NY 1996.

2 – H. C. Kang; J.Non-Cryst. Solids, 261, 169 (2000)

3 – O. V. Balachova, M. A. R. Alves, J. W. Swart, E. S. Braga e L. Cescato; Microelectronics Journal, 31, 213 (2000)

4 - I. Chambouleyron e A. R. Zanatta; Journal Appl. Phys. 84, 1 (1998).

CNPq